Precomptued Analysis

Use precomputed optimal angles to measure the expected value of \(\langle C \rangle\) across a variety of problem types, sizes, \(p\)-depth, and random instances.

Load in Raw Data

Go through each record, load in supporting objects, flatten everything into records, and put into a massive dataframe.

import recirq
import cirq
import numpy as np
import pandas as pd
from recirq.qaoa.experiments.precomputed_execution_tasks import \
    DEFAULT_BASE_DIR, DEFAULT_PROBLEM_GENERATION_BASE_DIR, DEFAULT_PRECOMPUTATION_BASE_DIR

records = []
for record in recirq.iterload_records(dataset_id="2020-03-tutorial", base_dir=DEFAULT_BASE_DIR):
    dc_task = record['task']
    apre_task = dc_task.precomputation_task
    pgen_task = apre_task.generation_task

    problem = recirq.load(pgen_task, base_dir=DEFAULT_PROBLEM_GENERATION_BASE_DIR)['problem']
    record['problem'] = problem.graph
    record['problem_type'] = problem.__class__.__name__
    record['optimum'] = recirq.load(apre_task, base_dir=DEFAULT_PRECOMPUTATION_BASE_DIR)['optimum']
    record['bitstrings'] = record['bitstrings'].bits
    recirq.flatten_dataclass_into_record(record, 'task')
    recirq.flatten_dataclass_into_record(record, 'precomputation_task')
    recirq.flatten_dataclass_into_record(record, 'generation_task')
    recirq.flatten_dataclass_into_record(record, 'optimum')
    records.append(record)
df_raw = pd.DataFrame(records)
df_raw['timestamp'] = pd.to_datetime(df_raw['timestamp'])
df_raw.head()

	timestamp	bitstrings	qubits	final_qubits	circuit	violation_indices	problem	problem_type	dataset_id	device_name	...	generation_task.dataset_id	generation_task.device_name	instance_i	n_qubits	optimum.p	f_val	gammas	betas	min_c	max_c
0	2020-04-08 13:11:32.151452	[[0, 0, 0, 0], [0, 0, 1, 0], [1, 1, 1, 1], [0,...	[(5, 3), (6, 2), (6, 3), (6, 4)]	[(5, 3), (6, 2), (6, 3), (6, 4)]	[(PhX(-0.824)^0.5((5, 3)), PhX(-0.824)^0.5((6,...	[]	(2, 0, 1, 3)	HardwareGridProblem	2020-03-tutorial	Syc23-simulator	...	2020-03-tutorial	Sycamore23	4	4	2	-2.616073	[0.47109541452232295, 0.5900885654628348]	[-0.44860990386986666, -0.29400122107756244]	-3.0	3.0
1	2020-04-08 13:11:32.520129	[[0, 1, 1, 0], [0, 0, 0, 1], [0, 0, 0, 0], [1,...	[(5, 3), (6, 2), (6, 3), (6, 4)]	[(5, 3), (6, 2), (6, 3), (6, 4)]	[(PhX(-0.644)^0.39663553581308286((5, 3)), PhX...	[]	(2, 0, 1, 3)	HardwareGridProblem	2020-03-tutorial	Syc23-simulator	...	2020-03-tutorial	Sycamore23	4	4	3	-3.000000	[0.3047317419709853, 0.6664224586095869, 0.607...	[-0.5760240058080092, -0.36261585803438645, -0...	-3.0	3.0
2	2020-04-08 13:11:31.499590	[[0, 0, 0, 0], [1, 0, 1, 1], [0, 1, 0, 0], [1,...	[(5, 3), (6, 2), (6, 3), (6, 4)]	[(5, 3), (6, 2), (6, 3), (6, 4)]	[(PhX(0.806)^0.3587079604881125((5, 3)), PhX(0...	[]	(2, 0, 1, 3)	HardwareGridProblem	2020-03-tutorial	Syc23-simulator	...	2020-03-tutorial	Sycamore23	4	4	1	-1.632993	[0.4776585668842565]	[-0.3926990816996555]	-3.0	3.0
3	2020-04-08 13:11:31.077127	[[1, 0], [1, 0], [0, 1], [1, 0], [1, 0], [1, 0...	[(5, 3), (6, 3)]	[(5, 3), (6, 3)]	[(PhX(0.163)^0.27171459224559236((5, 3)), PhX(...	[]	(1, 0)	HardwareGridProblem	2020-03-tutorial	Syc23-simulator	...	2020-03-tutorial	Sycamore23	4	2	2	-1.000000	[0.6283182637521854, 0.7853973288957912]	[-0.3926989532796281, -0.07854016690845925]	-1.0	1.0
4	2020-04-08 13:11:31.247321	[[1, 0], [1, 0], [0, 1], [0, 1], [0, 1], [1, 0...	[(5, 3), (6, 3)]	[(5, 3), (6, 3)]	[(PhX(-0.14)^0.5((5, 3)), PhX(-0.5)^0.5((6, 3)...	[]	(1, 0)	HardwareGridProblem	2020-03-tutorial	Syc23-simulator	...	2020-03-tutorial	Sycamore23	4	2	3	-1.000000	[0.5620701143250424, 0.7076351823020001, 0.798...	[-0.4199391572618354, -0.1086414306397252, -0....	-1.0	1.0

5 rows × 25 columns

Narrow down to Relevant Data

Drop unnecessary metadata and use bitstrings to compute the expected value of the energy. In general, it’s better to save the raw data and lots of metadata so we can use it if it becomes necessary in the future.

from recirq.qaoa.simulation import hamiltonian_objectives, hamiltonian_objective_avg_and_err
import cirq.google as cg

def compute_energy_w_err(row):
    permutation = []
    for i, q in enumerate(row['qubits']):
        fi = row['final_qubits'].index(q)
        permutation.append(fi)

    energy, err = hamiltonian_objective_avg_and_err(row['bitstrings'], row['problem'], permutation)
    return pd.Series([energy, err], index=['energy', 'err'])


# Start cleaning up the raw data
df = df_raw.copy()

# Don't need these columns for present analysis
df = df.drop(['gammas', 'betas', 'circuit', 'violation_indices',
              'precomputation_task.dataset_id',
              'generation_task.dataset_id',
              'generation_task.device_name'], axis=1)

# p is specified twice (from a parameter and from optimum)
assert (df['optimum.p'] == df['p']).all()
df = df.drop('optimum.p', axis=1)

# Compute energies
df = df.join(df.apply(compute_energy_w_err, axis=1))
df = df.drop(['bitstrings', 'qubits', 'final_qubits', 'problem'], axis=1)

# Normalize
df['energy_ratio'] = df['energy'] / df['min_c']
df['err_ratio'] = df['err'] * np.abs(1/df['min_c'])
df['f_val_ratio'] = df['f_val'] / df['min_c']

df

	timestamp	problem_type	dataset_id	device_name	n_shots	structured	echoed	p	instance_i	n_qubits	f_val	min_c	max_c	energy	err	energy_ratio	err_ratio	f_val_ratio
0	2020-04-08 13:11:32.151452	HardwareGridProblem	2020-03-tutorial	Syc23-simulator	50000	True	False	2	4	4	-2.616073	-3.0	3.0	-1.89004	0.007524	0.630013	0.002508	0.872024
1	2020-04-08 13:11:32.520129	HardwareGridProblem	2020-03-tutorial	Syc23-simulator	50000	True	False	3	4	4	-3.000000	-3.0	3.0	-1.85736	0.007451	0.619120	0.002484	1.000000
2	2020-04-08 13:11:31.499590	HardwareGridProblem	2020-03-tutorial	Syc23-simulator	50000	True	False	1	4	4	-1.632993	-3.0	3.0	-1.39456	0.007291	0.464853	0.002430	0.544331
3	2020-04-08 13:11:31.077127	HardwareGridProblem	2020-03-tutorial	Syc23-simulator	50000	True	False	2	4	2	-1.000000	-1.0	1.0	-0.89096	0.002031	0.890960	0.002031	1.000000
4	2020-04-08 13:11:31.247321	HardwareGridProblem	2020-03-tutorial	Syc23-simulator	50000	True	False	3	4	2	-1.000000	-1.0	1.0	-0.85592	0.002313	0.855920	0.002313	1.000000
...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...	...
145	2020-04-08 13:08:23.360051	SKProblem	2020-03-tutorial	Syc23-simulator	50000	True	False	3	0	7	-7.888209	-9.0	11.0	-1.53480	0.020784	0.170533	0.002309	0.876468
146	2020-04-08 13:08:16.029073	SKProblem	2020-03-tutorial	Syc23-simulator	50000	True	False	1	0	7	-5.318905	-9.0	11.0	-3.02000	0.019369	0.335556	0.002152	0.590989
147	2020-04-08 13:09:02.773520	SKProblem	2020-03-tutorial	Syc23-simulator	50000	True	False	2	1	7	-6.942368	-9.0	11.0	-2.36920	0.020491	0.263244	0.002277	0.771374
148	2020-04-08 13:09:06.524879	SKProblem	2020-03-tutorial	Syc23-simulator	50000	True	False	3	1	7	-7.888209	-9.0	11.0	-1.50696	0.020841	0.167440	0.002316	0.876468
149	2020-04-08 13:08:59.681882	SKProblem	2020-03-tutorial	Syc23-simulator	50000	True	False	1	1	7	-5.318905	-9.0	11.0	-3.04136	0.019464	0.337929	0.002163	0.590989

150 rows × 18 columns

Plots

%matplotlib inline
from matplotlib import pyplot as plt

import seaborn as sns
sns.set_style('ticks')

plt.rc('axes', labelsize=16, titlesize=16)
plt.rc('xtick', labelsize=14)
plt.rc('ytick', labelsize=14)
plt.rc('legend', fontsize=14, title_fontsize=16)

# theme colors
QBLUE = '#1967d2'
QRED = '#ea4335ff'
QGOLD = '#fbbc05ff'
QGREEN = '#34a853ff'

QGOLD2 = '#ffca28'
QBLUE2 = '#1e88e5'

C = r'\langle C \rangle'
CMIN = r'C_\mathrm{min}'
COVERCMIN = f'${C}/{CMIN}$'

def percentile(n):
    def percentile_(x):
        return np.nanpercentile(x, n)
    percentile_.__name__ = 'percentile_%s' % n
    return percentile_

Raw swarm plots of all data

import numpy as np
from matplotlib import pyplot as plt

pretty_problem = {
    'HardwareGridProblem': 'Hardware Grid',
    'SKProblem': 'SK Model',
    'ThreeRegularProblem': '3-Regular MaxCut'
}

for problem_type in ['HardwareGridProblem', 'SKProblem', 'ThreeRegularProblem']:
    df1 = df
    df1 = df1[df1['problem_type'] == problem_type]

    for p in sorted(df1['p'].unique()):
        dfb = df1
        dfb = dfb[dfb['p'] == p]
        dfb = dfb.sort_values(by='n_qubits')

        plt.subplots(figsize=(7,5))

        n_instances = dfb.groupby('n_qubits').count()['energy_ratio'].unique()
        if len(n_instances) == 1:
            n_instances = n_instances[0]
            label = f'{n_instances}'
        else:
            label = f'{min(n_instances)} - {max(n_instances)}'

        #sns.boxplot(dfb['n_qubits'], dfb['energy_ratio'], color=QBLUE, saturation=1)
        #sns.boxplot(dfb['n_qubits'], dfb['f_val_ratio'], color=QGREEN, saturation=1)
        sns.swarmplot(dfb['n_qubits'], dfb['energy_ratio'], color=QBLUE)
        sns.swarmplot(dfb['n_qubits'], dfb['f_val_ratio'], color=QGREEN)

        plt.axhline(1, color='grey', ls='-')
        plt.axhline(0, color='grey', ls='-')

        plt.title(f'{pretty_problem[problem_type]}, {label} instances, p={p}')
        plt.xlabel('# Qubits')
        plt.ylabel(COVERCMIN)
        plt.tight_layout()
        plt.show()

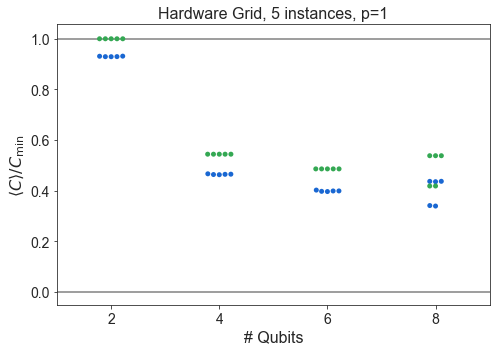
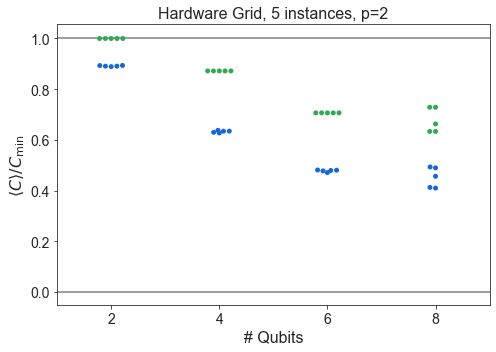
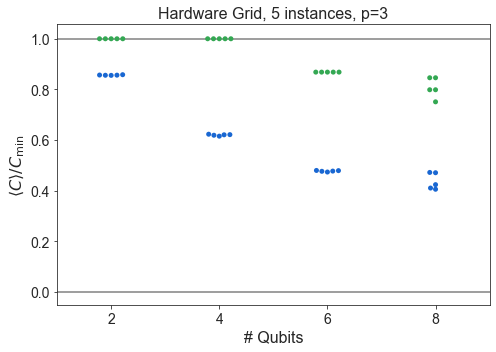
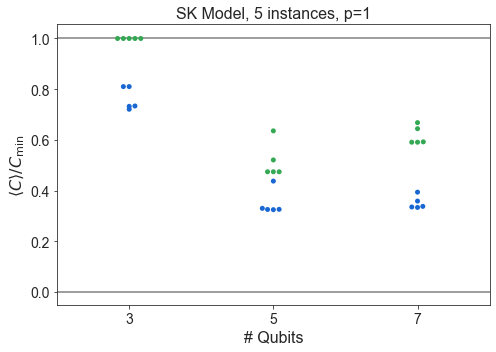
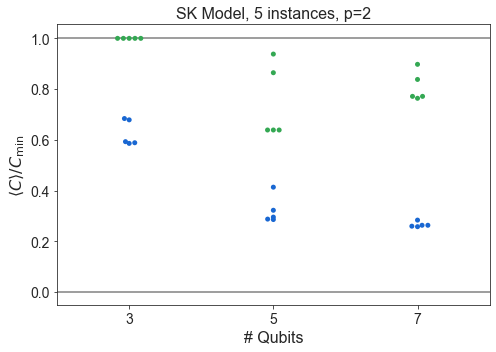
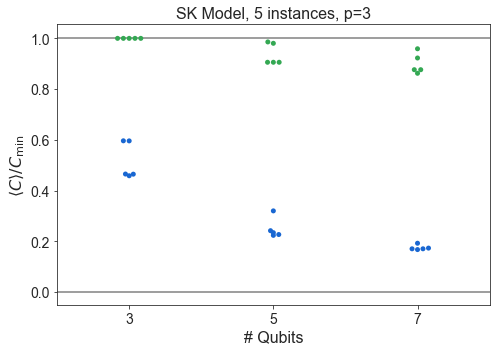
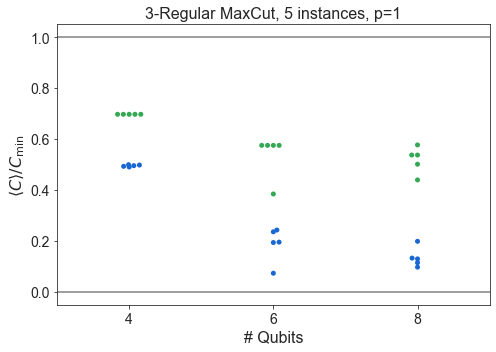
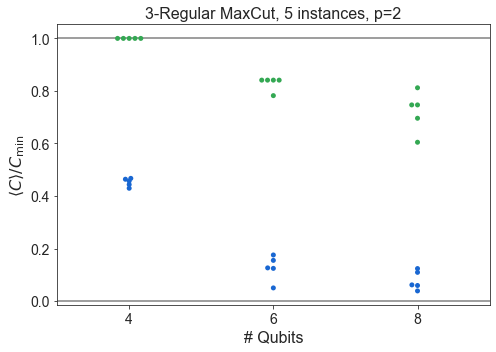
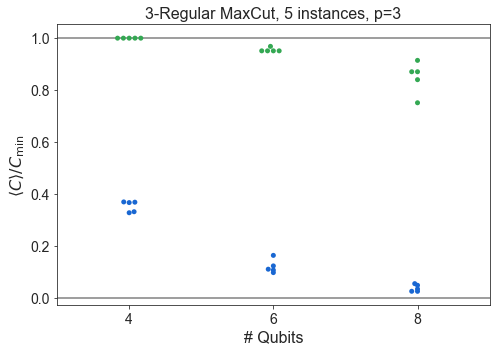
Compare SK and Hardware Grid vs. \(n\)

pretty_problem = {
    'HardwareGridProblem': 'Hardware Grid',
    'SKProblem': 'SK Model',
    'ThreeRegularProblem': '3-Regular MaxCut'
}

df1 = df
df1 = df1[
    ((df1['problem_type'] == 'SKProblem') & (df1['p'] == 3))
    | ((df1['problem_type'] == 'HardwareGridProblem') & (df1['p'] == 3))
    ]
df1 = df1.sort_values(by='n_qubits')

MINQ = 3
df1 = df1[df1['n_qubits'] >= MINQ]

plt.subplots(figsize=(8, 6))
plt.xlim((8, 23))

# SK
dfb = df1
dfb = dfb[dfb['problem_type'] == 'SKProblem']
sns.swarmplot(dfb['n_qubits'], dfb['energy_ratio'], s=5, linewidth=0.5, edgecolor='k', color=QRED)
sns.swarmplot(dfb['n_qubits'], dfb['f_val_ratio'], s=5, linewidth=0.5, edgecolor='k', color=QRED,
              marker='s')
dfg = dfb.groupby('n_qubits').mean().reset_index()
# --------


# Hardware
dfb = df1
dfb = dfb[dfb['problem_type'] == 'HardwareGridProblem']
sns.swarmplot(dfb['n_qubits'], dfb['energy_ratio'], s=5, linewidth=0.5, edgecolor='k', color=QBLUE)
sns.swarmplot(dfb['n_qubits'], dfb['f_val_ratio'], s=5, linewidth=0.5, edgecolor='k', color=QBLUE,
              marker='s')
dfg = dfb.groupby('n_qubits').mean().reset_index()
# -------


plt.axhline(1, color='grey', ls='-')
plt.axhline(0, color='grey', ls='-')

plt.xlabel('# Qubits')
plt.ylabel(COVERCMIN)

from matplotlib.patches import Patch
from matplotlib.lines import Line2D
from matplotlib.legend_handler import HandlerTuple

lelements = [
    Line2D([0], [0], color=QBLUE, marker='o', ms=7, ls='', ),
    Line2D([0], [0], color=QRED, marker='o', ms=7, ls='', ),

    Line2D([0], [0], color='k', marker='s', ms=7, ls='', markerfacecolor='none'),
    Line2D([0], [0], color='k', marker='o', ms=7, ls='', markerfacecolor='none'),
]

plt.legend(lelements, ['Hardware Grid', 'SK Model', 'Noiseless', 'Experiment', ], loc='best',
           title=f'p = 3',
           handler_map={tuple: HandlerTuple(ndivide=None)}, framealpha=1.0)
plt.tight_layout()
plt.show()

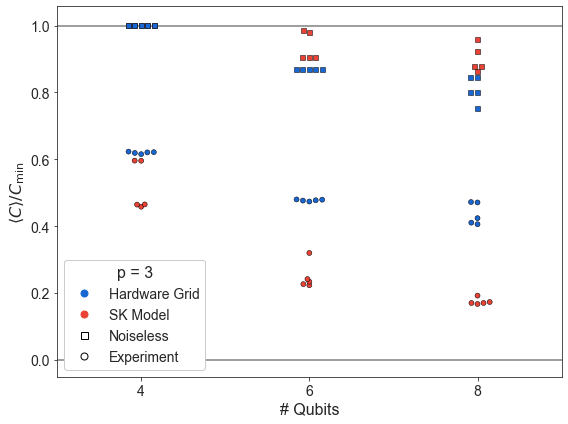
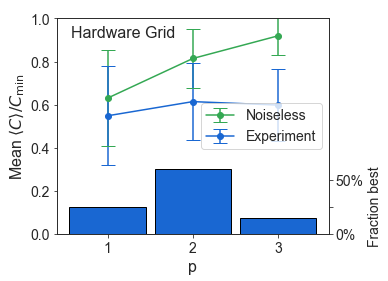
Hardware Grid vs. \(p\)

dfb = df
dfb = dfb[dfb['problem_type'] == 'HardwareGridProblem']
dfb = dfb[['p', 'instance_i', 'n_qubits', 'energy_ratio', 'f_val_ratio']]
P_LIMIT = max(dfb['p'])

def max_over_p(group):
    i = group['energy_ratio'].idxmax()
    return group.loc[i][['energy_ratio', 'p']]

def count_p(group):
    new = {}
    for i, c in enumerate(np.bincount(group['p'], minlength=P_LIMIT+1)):
        if i == 0:
            continue
        new[f'p{i}'] = c
    return pd.Series(new)


dfgy = dfb.groupby(['n_qubits', 'instance_i']).apply(max_over_p).reset_index()
dfgz = dfgy.groupby(['n_qubits']).apply(count_p).reset_index()
# In the paper, we restrict to n > 10
# dfgz = dfgz[dfgz['n_qubits'] > 10]
dfgz = dfgz.set_index('n_qubits').sum(axis=0)
dfgz /= (dfgz.sum())
dfgz

p1    0.25
p2    0.60
p3    0.15
dtype: float64

dfb = df
dfb = dfb[dfb['problem_type'] == 'HardwareGridProblem']
dfb = dfb[['p', 'instance_i', 'n_qubits', 'energy_ratio', 'f_val_ratio']]
# In the paper, we restrict to n > 10
# dfb = dfb[dfb['n_qubits'] > 10]
dfg = dfb.groupby('p').agg(['median', percentile(25), percentile(75), 'mean', 'std']).reset_index()

plt.subplots(figsize=(5.5,4))
plt.errorbar(x=dfg['p'], y=dfg['f_val_ratio', 'mean'],
             yerr=(dfg['f_val_ratio', 'std'],
                   dfg['f_val_ratio', 'std']),
             fmt='o-',
             capsize=7,
             color=QGREEN,
             label='Noiseless'
           )
plt.errorbar(x=dfg['p'], y=dfg['energy_ratio', 'mean'],
             yerr=(dfg['energy_ratio', 'std'],
                   dfg['energy_ratio', 'std']),
             fmt='o-',
             capsize=7,
             color=QBLUE,
             label='Experiment'
           )
plt.xlabel('p')
plt.ylabel('Mean ' + COVERCMIN)
plt.ylim((0, 1))
plt.text(0.05, 0.9, r'Hardware Grid', fontsize=16, transform=plt.gca().transAxes, ha='left', va='bottom')
plt.legend(loc='center right')

ax2 = plt.gca().twinx()  # instantiate a second axes that shares the same x-axis

dfgz_p = [int(s[1:]) for s in dfgz.index]
dfgz_y = dfgz.values
ax2.bar(dfgz_p, dfgz_y, color=QBLUE, width=0.9, lw=1, ec='k')
ax2.tick_params(axis='y')
ax2.set_ylim((0, 2))
ax2.set_yticks([0, 0.25, 0.50])
ax2.set_yticklabels(['0%', None, '50%'])
ax2.set_ylabel('Fraction best' + ' ' * 41, fontsize=14)

plt.tight_layout()